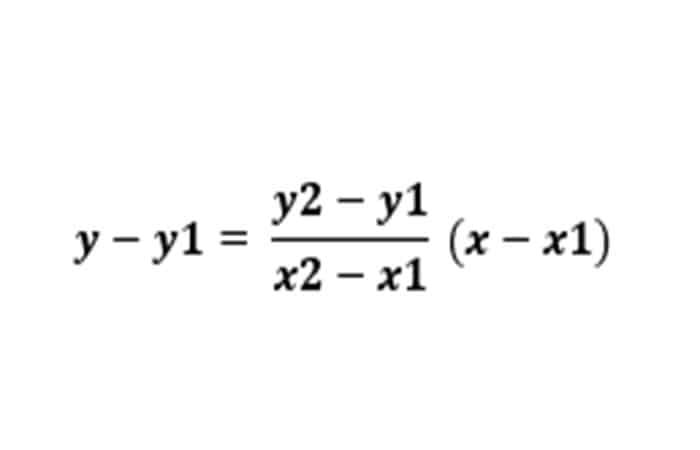Formula de la interpolacion

Interpolación de lagrange

El término «interpolación» se refiere a la técnica de ajuste de curvas que se utiliza en la predicción de valores intermedios y patrones sobre la base de los datos históricos disponibles junto con los puntos de datos recientes. En otras palabras, la técnica de interpolación puede utilizarse para predecir los puntos de datos que faltan entre los puntos de datos disponibles.
La fórmula de la interpolación consiste básicamente en construir una función para la variable desconocida (y) a partir de la variable independiente y de al menos dos puntos de datos: (x1, y1) y (x2, y2). Matemáticamente, se representa como,
Tomemos el ejemplo de una Varilla caliente para ilustrar el concepto de interpolación. Supongamos que la temperatura de la varilla era de 100°C a las 9.30 A.M. y que gradualmente bajó a 35°C a las 10.00 A.M. Encuentre la temperatura de la varilla a las 9.40 A.M. basándose en la información dada.
Tomemos el curioso caso de Juan Pérez, que ha ganado mucho peso en los últimos meses. Por ello, su médico ha decidido controlar su peso y ha iniciado un seguimiento de su peso cada 6 días durante los últimos 60 días. Se ha recogido la siguiente información:

Fórmula de interpolación – stirling, gauss hacia delante y hacia atrás

dentro del prisma rectangular axial local de forma lineal, utilizando los datos de la función en los puntos de la malla. Para una malla arbitraria y no estructurada (como la utilizada en el análisis de elementos finitos), deben utilizarse otros métodos de interpolación; si todos los elementos de la malla son tetraedros (símiles 3D), las coordenadas baricéntricas proporcionan un procedimiento sencillo.
Los valores adyacentes predefinidos que rodean el punto de interpolación. Hay varias formas de llegar a la interpolación trilineal, que equivale a la interpolación tensorial B-spline tridimensional de orden 1, y el operador de interpolación trilineal es también un producto tensorial de 3 operadores de interpolación lineal.
Una visualización geométrica de la interpolación trilineal. El producto del valor en el punto deseado y el volumen completo es igual a la suma de los productos del valor en cada esquina y el volumen parcial diagonalmente opuesto a la esquina.

Fórmula de interpolación -newton hacia adelante y hacia atrás | ejemplo

Kathryn ha enseñado matemáticas en la escuela secundaria o en la universidad durante más de 10 años. Tiene un doctorado en Matemáticas Aplicadas por la Universidad de Wisconsin-Milwaukee, un máster en Matemáticas por la Universidad Estatal de Florida y una licenciatura en Matemáticas por la Universidad de Wisconsin-Madison.
¿Qué es la interpolación? La interpolación es el proceso de encontrar un valor entre dos puntos de una línea o curva. Para ayudarnos a recordar lo que significa, debemos pensar en la primera parte de la palabra, «inter», como si significara «entrar», lo que nos recuerda que debemos mirar «dentro» de los datos que teníamos originalmente. Esta herramienta, la interpolación, no sólo es útil en la estadística, sino también en la ciencia, en los negocios o en cualquier momento en que sea necesario predecir valores que se encuentren dentro de dos puntos de datos existentes.
Ejemplo de interpolaciónAquí hay un ejemplo que ilustrará el concepto de interpolación. Una jardinera ha plantado una planta de tomate y ha medido y registrado su crecimiento cada dos días. Esta jardinera es una persona curiosa, y le gustaría estimar la altura de su planta al cuarto día. Su tabla de observaciones tenía el siguiente aspecto:

Fórmula de interpolación de newton mejor y más fácil ejemplo(parte-2

La interpolación bilineal se realiza mediante una interpolación lineal primero en una dirección y luego en la otra. Aunque cada paso es lineal en los valores muestreados y en la posición, la interpolación en su conjunto no es lineal sino cuadrática en la ubicación de la muestra.
Supongamos que queremos encontrar el valor de la función desconocida f en el punto (x, y). Se supone que conocemos el valor de f en los cuatro puntos Q11 = (x1, y1), Q12 = (x1, y2), Q21 = (x2, y1) y Q22 = (x2, y2).
{\displaystyle {\begin{aligned}a_{0}&={\frac {f(Q_{11})x_{2}y_{2}}{(x_{1}-x_{2})(y_{1}-y_{2})}}+{\frac {f(Q_{12})x_{2}y_{1}}{(x_{1}- x_{2})(y_{2}-y_{1})}}+{\frac {f(Q_{21})x_{1}y_{2}}{(x_{1}-x_{2})(y_{2}-y_{1})}}+{\frac {f(Q_{22})x_{1}y_{1}}{(x_{1}-x_{2})(y_{1}-y_{2})}}, \\a_{1}&={\frac {f(Q_{11})y_{2}}{(x_{1}-x_{2})(y_{2}-y_{1})}}+{\frac {f(Q_{12})y_{1}}{(x_{1}-x_{2})(y_{1}- y_{2})}}+{\frac {f(Q_{21})y_{2}}{(x_{1}-x_{2})(y_{1}-y_{2})}}+{\frac {f(Q_{22})y_{1}}{(x_{1}-x_{2})(y_{2}-y_{1})}}, \\a_{2}&={\frac {f(Q_{11})x_{2}}{(x_{1}-x_{2})(y_{2}-y_{1})}}+{\frac {f(Q_{12})x_{2}}{(x_{1}-x_{2})(y_{1}- y_{2})}}+{\frac {f(Q_{21})x_{1}}{(x_{1}-x_{2})(y_{1}-y_{2})}}+{\frac {f(Q_{22})x_{1}}{(x_{1}-x_{2})(y_{2}-y_{1})}}, \\a_{3}&={\frac {f(Q_{11})}{(x_{1}-x_{2})(y_{1}-y_{2})}}+{\frac {f(Q_{12})}{(x_{1}-x_{2})(y_{2}- y_{1})}}+{\frac {f(Q_{21})}{(x_{1}-x_{2})(y_{2}-y_{1})}}+{\frac {f(Q_{22})}{(x_{1}-x_{2})(y_{1}-y_{2})}}. \nd{aligned}}